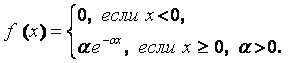Магазин решенных задач:
Непрерывная случайная величина:
стр. 1 2 3 4 5 6 7 8 9 10 11 12 13 14
90100. Случайные величины х и у независимы, х равномерно распределена на [0, 1], у распределена по нормальному закону с параметрами а = 0 и s = 1. Найдите композицию законов распределения х и у, т.е. закон распределения величины z = х +у.
90101. Случайная величина х имеет плотность вероятности (показательный закон распределения). Найдите математические ожидания величин х и у = 2х2 +3.
90102. Известно, что М[х] = 2, М[у] = 1,5. Найдите математическое ожидание величины z = 3x – y + 2,5.
90103. Случайная величина Х распределена по нормальному закону, причём М(Х) = 10, D(X) = 9. Найти: 1) P{7 < X < 11}; 2) P{0 < X < 12}.
90104. Известно, что случайные величины Х и Y независимы, причем D(X)=4,D(Y)=3. Найти D(3X), D(-4X), D(X+Y)
90105. Непрерывная случайная величина имеет нормальное распределение. Ее математическое ожидание равно 50, среднее квадратичное отклонение равно 6. Найти вероятность того, что в результате испытания случайная величина примет значение в интервале (48;53)
90106. Вес товаров, помещаемых в контейнер определенного размера, -нормально распределенная случайная величина. Известно, что 65% контейнеров имеют чистый вес больше чем 4,9т и 25% - меньше чем 4,2т.Найдите ожидаемый средний вес и среднее квадратическое отклонение чистого веса контейнеров.
90107. Случайная величина имеет нормальное распределение с а=56, и среднем квадратичным отклонением =8, найти интервал симметричный относительно мат. ожидания вероятность попадания в который P=0.95
90108. Случайные величины X и Y независимы и нормально распределены с параметрами
и
. Найти коэффициент корреляции случайных величин 8X+9Y и 8X-9Y.
90109. Имеются две случайные величины Х и Y, связанные линейной зависимостью Y=5+3X. Числовые характеристики случайной величины Х заданы: М(Х)=0, D(X)=5.
Найти - 1) ковариацию с.в. Х и Y; 2) коэффициент корреляции с.в. X и Y.