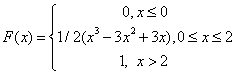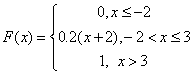Магазин решенных задач:
Непрерывная случайная величина:
стр. 1 2 3 4 5 6 7 8 9 10 11 12 13 14
90080. Дана случайная величина Х подчиненная нормальному распределению с параметрами: среднее значения а=7, и стандартное отклонение σ=2. Найти вероятность попадания случайной величины Х в интервал (3;10)
90081. Из партии с нормально распределенным параметром Х извлечена выборка объемом n=40. Среднее квадратическое отклонение параметра Х в партии = σ=3, среднее значение параметра Х в выборке
=15. При доверительной вероятности γ=0,85 найти доверительный интервал
90082. Предпологается, что в партии изделий с нормально распределенным параметром Х. Среднее значение этого параметра μ=12. Производится n=25 замеров в результате которых среднее выборочное значение исследуемого признака оказалось равным
=0,07 выполнить проверку нулевой гипотезы
90083.Фунция распределения с. в. X имеет вид. Найти вероятность p=P(1<X<2) и M(X).
90084. Случайная величина Х имеет плотность распределения вида. Найти константу С, вероятность того что Х>2 и математическое ожидание случайной величины Х
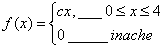
90085, Случайная величина Х имеет нормальный закон распределения с параметрами α и σ в квадрате. Найти эти параметры, если известно, что вероятности P(x<1)=0,5 и P(-2<4)=0,9973.Вычислить вероятность того, что случайная величина Х примет значение меньше 2.
90086. Случайная величина распределена по закону
при (х>0). Найти математическое ожидание, дисперсию и стандартное отклонение. Найти вероятность, что случайная величина попадет в интервал (1,2)
90087. Случайная величина Х распределена нормально с параметрами µ=0 и σ=0,75. Найти вероятность, что случайная величина попадет в интервал [0;3]. Найти вероятность, что отклонение Х от µ по абсолютному значению не превысит 1,5.
90088. В телеателье за 8 часов рабочего времени получают 32 заявки. Какова вероятность, что ателье в течении 2 часов получит 9 заявок?
90089. Случайная величина задана функцией распределения. Найти числовые характеристики случайной величины X: M(X),D(X), P(1<X<5).
